Entanglement is one of the main aspects of quantum mechanics. It attracts extensive investigations. The entanglement of two subsystems in a bipartite system is a very important feature which finds extensive application in quantum computing, communication, and information processing. One of the standard measures of bipartite entanglement is the subsystem von Neumann entropy.
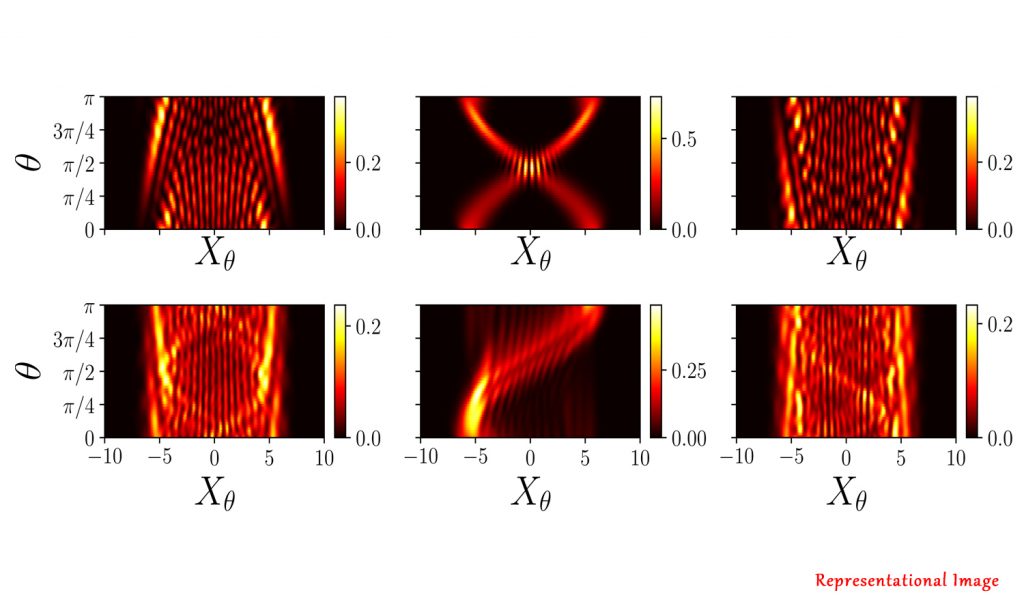
Quantum tomograms are analogs of medical images and scans. A tomogram is a collection of histograms (a histogram is a diagram of rectangles whose area is proportional to the frequency of a variable). Quantum state reconstruction seeks to obtain the density matrix from the tomogram. However, this process tends to be tedious and complex for optical systems. Reconstruction of the optical state from appropriate tomograms poses several challenges even today. In particular the measurement of the subsystem von Neumann entropy requires knowledge of the full density matrix. Because of this, it has been suggested to read off information about a state directly from the tomograms. For instance, estimation of quantum entanglement through manipulations of the relevant tomograms alone would be considered sufficient.
The tomographic approach in continuous-variable (CV) systems has several advantages. An example is in identifying qualitative signatures of entanglement between the radiation fields in the output ports of a quantum beamsplitter. Further, quantitative analysis of entanglement can be done directly from tomograms, circumventing detailed state reconstruction.



In this paper, the authors (B. Sharmila, presently in University of Warwick, Coventry, UK, and S. Lakshmibala and V. Balakrishnan, both from the Department of Physics, Indian Institute of Technology (IIT) Madras, Chennai, India) have investigated CV systems and quantified bipartite entanglement.
These systems are:
- Entangled Talbot carpets
- Entangled biphoton frequency combs
The authors have established that tomographic entanglement indicators are very useful tools in determining the extent of entanglement. These indicators have been employed to estimate the degree of entanglement between a pair of Talbot carpets. This procedure is simpler and more direct than the standard state reconstruction method. The authors have also established that the tomograms corresponding to two biphoton frequency combs carry clear entanglement signatures that distinguish between their corresponding quantum states. In fact, a single slice of an appropriate tomogram has been proved in this paper to be sufficient to estimate the extent of entanglement. This paper shows that the tomographic approach is a good alternative to long-winded, cumbersome state reconstruction programs. It is useful and efficient in a variety of experiments in CV systems.
Prof. Prasanta K. Panigrahi from the Indian Institute of Science Education and Research (IISER), Kolkata, India, acknowledged the importance of the work done by the authors by giving the following comments: “The understanding and quantification of the quantum property known as entanglement, indicative of non-separability of the constituents of a wave function, are the key areas of the present day research in quantum information theory. For finite dimensional systems, entanglement has been quantified and used for counterintuitive tasks like teleportation. For continuous variable states of light, the authors not only entangle the quantum carpets, but also show how to quantify it through tomographic means. Tomography has played a key role in imaging; the present approach can find analogous application and use for a better understanding of quantumness.”
Article by Akshay Anantharaman
Here is the original link to the paper:
https://iopscience.iop.org/article/10.1088/1361-6455/ac870d