Security has become a major necessity to protect and safeguard our valuable information. Consider the security for a joint bank locker which involves 2 or 3 people sharing and accessing information jointly. One needs trustworthy people for such access.
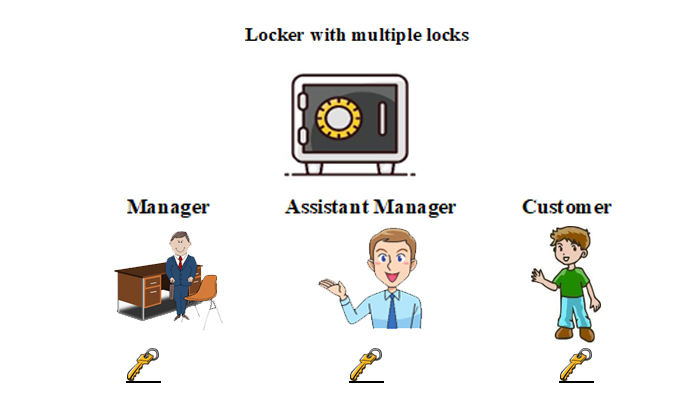
To increase the security of the bank locker, only 3 people are given a key – the bank manager, the assistant bank manager, and the customer. The locker will have 3 locks, and each lock can be accessed by a single key. But in order to open the locker, all 3 keys must be used at the same time.
All 3 – the manager, the assistant manager, and the customer must get together to open the locker. Even if one key is not used, the locker cannot be opened.
The above example about the bank locker shows a common occurrence of secret sharing. In a more general case of secret sharing, there are a number of parties out of which say a quorum of k parties come together to solve a secret. This is done in such a way that a lesser k number of parties should not have access to the secret.
Secret sharing can be used for sharing information between multiple parties securely. Here, instead of physical valuables it is information that is being protected.
In today’s computers, information is stored in the form of bits. Bits are represented by ‘1’s and ‘0’s.
In classical information, the value of a bit can be either ‘1’ or ‘0’. But quantum information can be ‘1’ and ‘0’ at the same time.
While classical information can be downloaded separately and can be copied, this is not the case for quantum information. The no-cloning theorem states that quantum information cannot be copied like classical information.
In this study, by Mr. Kaushik Senthoor and Prof. Pradeep Sarvepalli from the Department of Electrical Engineering, Indian Institute of Technology Madras, Chennai, India, quantum secret sharing is studied. Quantum secret sharing has many applications in the field of distributed and secure computing with quantum information. Quantum secret sharing schemes enable the sharing of quantum secrets.
The focus of this paper is on a class of quantum secret sharing schemes called communication efficient threshold quantum secret sharing (CE-QTS) schemes. Whenever a secret is recovered, a communication cost occurs which is preferred to be low. When the secret sharing protocol is used to share multiple secrets, the communication costs multiply. This study aims to reduce these quantum communication costs. In these schemes instead of the whole information with a party, only a part of the information is shared during recovery to reduce the communication cost.
Communication efficient quantum secret sharing schemes are constructed here by using a technique called concatenation and by using staircase codes.
In the standard model of quantum secret sharing, when the secret is recovered from any k parties, the communication cost is at least k times the size of the secret. The problem the authors solve here is how to reduce this communication cost by allowing more than the necessary number of parties, say some d>k parties. This provides a flexibility to the combiner to access (i) any k parties for the standard secret recovery or (ii) any d parties for communication efficient secret recovery. Using quantum information theoretic arguments, they were able to show the optimality of the proposed schemes.

Consider an example where there are only 3 parties who share a secret, namely Alice, Bob, and Carol.
In this, Alice, Bob, and Carol each have 2 bits, or 2 quantum digits (qudits) of information. Any 2 parties can come together to recover the information or the secret.
However, in communication efficient threshold quantum secret sharing schemes (CE-QTS), each party is allowed to share only a part of the information.

Here, the party Alice shares only 1 qudit of information, not the entire 2 qudits. Similarly, Bob and Carol also share only a part of the information they have. This helps to reduce the communication cost by accessing more than the minimum number of parties and through partial download. In the previous scheme, 4 qudits were needed to recover the secret, whereas here we need only 3.
In this study, another scheme is introduced called universal communication efficient threshold quantum secret sharing scheme (Universal CE-QTS). Instead of providing a single level of flexibility to reduce communication cost, universal CE-QTS reduces communication cost more as more and more parties participate in the recovery of the secret. This reduction in communication cost makes this scheme more efficient.
This paper proves that these constructions achieve optimal communication cost. Reduction in the communication cost and flexibility in secret recovery are important factors in quantum secret sharing. Less communication cost makes the proposed scheme efficient and better to use.
Prof. Marco Tomamichel from the Department of Electrical and Computer Engineering, National University of Singapore, explains the importance of this paper by giving the following comments: “Quantum secret sharing is a topic of ongoing interest in quantum information, and studies how a quantum state can be shared amongst n parties in such a way that any d ≥ k parties can recover the state when cooperating, but fewer cannot. This paper builds on previous work that shows how much communication between the legitimate parties is required to recover the state and in particular shows that the communication requirement drops when d > k. In this work the authors give an exact lower bound on the required communication and show that it can be achieved by universal codes. This settles an interesting problem in quantum secret sharing and might find applications on other areas of quantum information, where secret sharing is often used as a basic primitive.”
Article by Akshay Anantharaman
Here is the original link to the paper:
https://ieeexplore.ieee.org/document/9674910