Mathematics is a vast and endless field with several areas of specialization such as algebra, geometry, calculus, and many others. There is one area of mathematics called combinatorics that has been producing exciting and impactful results since time immemorial. Combinatorics generally deals with counting. Although this may sound simple, it has many, diverse applications in physics, biology, and computer science.
Combinatorics is used in pattern recognition and image processing techniques in computer science. In biology, it is used to study nucleotide sequencing in DNA computing. In physics, it is used in crystallography.
In Formal Languages, a word is a sequence of letters or symbols. Words can be finite or infinite. A tandem is a repetitive subword that occurs in a word. In computer science engineering, tandem-repeats are used in compression algorithms. In molecular biology and genealogical DNA tests, tandem-repeats are very useful to determine inherited traits of an individual.
In this study conducted by Mr. M. Sivasankar and Dr. R. Rama from the Department of Mathematics, Indian Institute of Technology Madras, Chennai, India, tandem-repeats have been studied in two-dimensional Fibonacci arrays.
In computer science, an array is a data structure that consists of a collection of values or variables. For example, a name, or a sequence of numbers could constitute a one dimensional array.
Fibonacci words/arrays are formed by repeated concatenation in the same way that Fibonacci numbers are formed by repeated addition. Recall that Fibonacci numbers are a sequence of numbers where each number is the sum of the two preceding ones. The initial sequence is as follows: 0, 1, 1, 2, 3, 5, 8, 13…
Fibonacci words are over any two-letter alphabet (usually over the binary digits). Two-dimensional arrays are an extension of one-dimensional arrays. In a one-dimensional array, a tandem-repeat for a non-empty string x, is xx. Finding a tandem-repeat in a two-dimensional array, which is of size m x n, where m is the number of rows, and n is the number of columns, is more complex. A tandem in a two-dimensional array, is a configuration consisting of a block W that touches with the same block W on the other side or its corner as shown below.
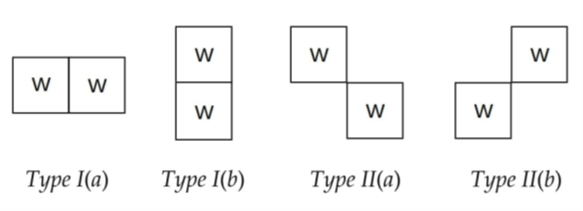
Figure: Types of tandems that can occur in a two-dimensional array
In this study, both the finite and the infinite two-dimensional Fibonacci arrays were studied. The exact number of tandems occurring in a two-dimensional Fibonacci array was counted, both with and without repetition. Factor complexity of finite two-dimensional Fibonacci arrays was also studied. It was also proved that infinite two-dimensional Fibonacci word is a morphic word. A DFAO (Deterministic Finite state Automaton with Output) generating the two-dimensional Fibonacci words was also constructed.
Some closely related properties to tandem-repeats are approximate tandem-repeats and approximate periodicity of two-dimensional Fibonacci words. These could be studied for future research.
Prof. Krishna Shankar Narayanan, from the Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Mumbai, India, gave her analysis of the work done by the authors with the following comments: “This article reports a very interesting result capturing the exact number of tandems in a given finite Fibonacci array of dimension m x n. Prior work in this direction is only known to provide an upper bound for the number of tandems of a certain type, but not the exact number. The authors obtain an expression capturing the exact number of tandems of both types in this paper by going through some non-trivial combinatorics, thereby finding the factor complexities of a given finite Fibonacci array. The generality of the proposed technique also allows one to use the same in computing the factor complexity of an infinite dimensional Fibonacci array as well.”
Article by Akshay Anantharaman
Click here for the original link to the paper